EZW算法简析
何琪辰 上海大学计算机工程与科学学院 10720955
heqichen(a)gmail.com
http://heqichen.cn
1．简介
EZW算法是1993年由Jerome M. Shapiro提出的基于小波变换的算法。该算法的结果能够经过熵编码后有很高的压缩效率。
E代表了Embedded。嵌入式编码就是渐进式编码。意思是先把最重要的部分进行编码，然后再将次要的部份进行编码。如果把一幅图像进行序列化，低频信号往往是占主要地位的。所以，进过小波变换之后的图像，把左上角放低频信号，右下角放高频信号。并且，编码的扫描线也是从左上方开始扫描，最后到右下角，这样来做到先将图像的重要信息进行编码。http://heqichen.cn
W代表了wavelet transform。图像在进入EZW编码器之前先要进行小波变换，分离高低频信息。所以EZW是基于小波变换的算法。
Z代表了Zerotree。称之为“零数”。到目前为止，没有对零树有统一的严格的定义。零树是EZW作者为了方便阐述其算法思想而构造的一种数据结构。并认为，若一棵树能满足特定的几点特定要求，就称之为零树。因为原为中对零数要求在文章中分得十分散，都是用到了再讲，我也没有时间来整理这方面的内容所以零数的具体定义我也没能给出。
文中提到的教材指清华大学出版社的《多媒体技术基础（第3版）》林福宗编著。
2．EZW的算法过程
要进行EZW编码，首先要完成一幅多分辨率图像上的建树操作，以最左上角的一个数为根节点，将与其相关的次级高频信号作为它的子树进行建树操作。
父-子节点对应关系如图 1左侧所示。
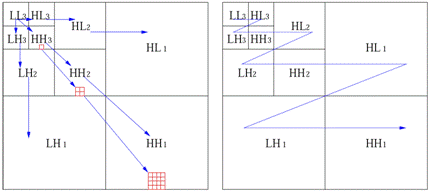
然后按照图 1右侧的顺序依次扫描图像上的数值，并通过EZW算法进行编码。每次扫描都将送出数据，但是前一次扫描的数据会比后一次扫描得到的数据更重要，数据是否重要，在EZW算法中体现的就是和一个设定的阈值相比较，若大于阈值，则是重要的数据，反之则不重要。
二维图像扫描的顺序也有很多种，如图 2所示，就是两种比较常用的扫描方法，上侧的叫光栅扫描，下测的称之为迂回扫描。使用不同的扫描方法得到的EZW编码会略有不同，对于需要压缩较高的场合，要根据实际情况选择合适的扫描方法进行编码。后文中的例子使用迂回扫描的方法进行的。
在EZW中，每次扫描的阈值都比上一次小一半，也就是上一次的阈值除以二得到新的阈值。之所以是两倍两倍减少，是因为在计算机中二进制算法更为简单，更为高效。这样的编码方式也称平面编码（bitplane coding）[3]。那么，在第一次扫描的时候就必须要决定阈值Th这个值的大小（这里使用Th代表阈值，避免和EZW符号集中的零树T相冲突）。Th不能太大，因为如果太大了，要减小很多次才能真正开始发送数据。这样最开始的几次计算就会浪费计算资源、消耗计算时间。同时Th也不能设置的过小，若太小，则第一次扫描就会将大部分数据发送出去，对于编码而言就毫无意义，所以必须要有一个最合适的值。并且符合下列不等式。
其中
表示图像上的所有数据值。显然，第一次扫描时一定会有数据被发送出去，所以
，同时这个值也不能太小，若比Th更大一级的阈值就不能满足这个情况。那么Th的值就是合适的。符合这样的数值就能备取为阈值。阈值的计算公式如下。http://heqichen.cn
[3]
由于Word的公式编辑器没法输入取下整符号，上面的公式我直接就拿人家的图片了，意思意思。
基于以上几个前提条件，就可以开始真正的EZW算法了。原文中的算法流程图指给出对于一个数值上来说输出符号的算法，没有整个算法的流程图，我这里给出这个算法的流程图。
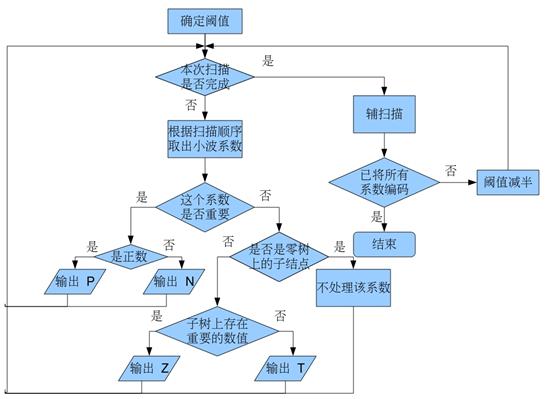
图 3 EZW算法流程图
3．EZW效果
如图 4所示是JPEG算法和JPEG2000算法的比较，JPEG2000采用的就是EZW算法。当他们采用相同的比特率时，明显JPEG2000的图像质量要比JPEG的图像质量好很多。
图 5所示的是采用 EZW算法编码后的解码过程，可以很清楚地看到，由于EZW是渐进式的编码过程，当或得到一部分数据后就能够将图像显示出来，只是图像的清晰度比较低，因为数据最开始的部分都是粗糙的数据，而越后得到的数据是越细节的数据。可以看当或得到细节数据后，图像就能够被逐步还原。
4．算法过程实例
算法的大致过程可以参考书上，但是量化的那几幅图我觉得可能对于初学者来说表示的不是很明确，而我感觉EZW算法的原文作者在文章中阐述的比较清晰，我根据原文的想法，然后采用类似线段数的方式表示的。由于我这些想法最开始的时候都是形成在纸上，没有很好的格式，输入电脑又比较麻烦，实验室项目催得比较紧，我只能大致上描述一下。见谅。http://heqichen.cn
对于编码过程，可以参考图 6所示的内容。例如，在阈值初始值选取32的情况下，主扫描会将所有的系数范围分为两个部份，一个部分是[0,32)，另一个部分是[32, 64)。若系数落在红色的可能输出符号T或者Z，根据具体情况而定。若落在蓝色部份则可能输出P或者N，根据系数的符号而定。在辅助扫描后，会将输出P或N的系数在进行细分，输出的值可以见图 6树枝上的数值。以此类推，这样就最终就能将细节信息毫无保留的发送出去。但是若某些情况对于图像要求不是很高的情况，只要将前几次的扫描结果进行解码操作就能得到图像的粗糙信息，如图 5所示。
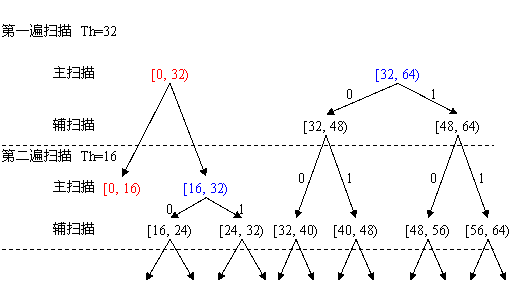
在解码过程中，若已经得知初始的阈值，则可以通过图 6所示的树得到某一位置上系数所属的范围，而在表现的时候，需要用一个值来代表这个范围，这个值就是这个范围的中间值，比如代表[48, 64)的值就是56。
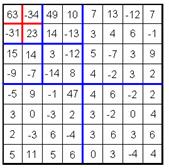
图 7所示是EZW原文中给出的实例。通过计算，得到符号序列如表格 1所示。
|
扫描名称 |
输出符号 |
|
D1 |
PNZTPTTTTZTTTTTTTPTT |
|
S1 |
1010 |
|
D2 |
ZTNPTTTTTTTT |
|
S2 |
1001 10 |
|
D3 |
ZZZZZPPNPPNTTNNPTPTTNTTTTTTTTPTTTPTTTTTTTTTPTTTTTTTTTTTT |
|
S3 |
1001 11 01111011011000 |
|
D4 |
ZZZZZZZTZTZNZZZZPTTPTPPTPNPTNTTTTTPTPNPPPPTTTTTPTPTTTPNP |
|
S4 |
1101 11 11011001000001 110110100010010101100 |
|
D5 |
ZZZZZTZZZZZTPZZZTTPTTTTNPTPPTTPTTTNPPNTTTTPNNPTTPTTPPTTT |
|
S5 |
1011 11 00110100010111 110101101100100000000 110110110011000111 |
|
D6 |
ZZZTTZTTTZTTTTTNNTTT |
第6次没有辅助扫描，因为在第五次的辅助扫描中，每个分段的长度已经达到1了，已经能够确定每个系数的具体值，所以不需要进行辅助编码。
5．关于教材上不妥当的地方
1.
图8-5
图中EZW算法结构被描述成三个模块，但是根据文中也指出了，这张图是说明小波图像编码的结构，但是在图下的题注中却写成了“EZW算法结构”
。EZW只是对小波变换完成后的多分辨率图像进行编码，不包括小波变换和熵编码。http://heqichen.cn
2.
建树的过程
由于EZW原文中也有对建树的过程有形式化的描述，只是上下级相关的数作为书的子节点。但是根据图像的层次结构、逻辑上的关系以及编程实现上的观点，我得出的结论是，LL3对应HL3、LH3、HH3三个节点，然后每个节点都对应到下一层的四个节点。之所以说树的地一层只有三个节点，因为，树的根没有再次分离高低频信息，而其余的点都是分离了高低频信息的，只有根节点是混合所有信息的，所以对于这个节点来说需要特殊处理。而根据教材上的观点，根有四个，然后每个根又对三个子节点，然后子节点又对应到四个更子的节点。这样分法对于扫描三阶图像来说是没问题的，但是对于更高阶的图像来说，明显是毫无规律的，从逻辑上讲无法成立，编程上也无法实现。作者也没有给出为什么这样建树的理由。所以我认为，这样建树的过程是不妥当的。
3. 主扫描之后是否要排序
书上对主扫描之后的结果进行了排序，但是必须要说明排序的规则是什么，书上没有说。在EZW原文中，是这样阐述的“those magnitudes are reordered for future subordinate passes in the
order(64, 49, 34, 47). Note that 49 is moved ahead of 34 because from the
decoder’s point of view, the reconstruction values 56 and 40 are
distinguishable. [1]”。没有说具体的排序规则，但是原文可以看出他是排序的。然而，排不排序实际上是无关紧要的，只要有一定规律就行了，比如用迂回扫描出的结果作为顺序，当然，这也是一种排序。但是书上写了一种莫名其妙的排序方法。
3. 前一次扫描出的重要数值，是否需要再次扫描
这个问题的话，是可以扫描，也可以不扫描，但是我自己的出的结果是，扫描比不扫描能够节省编码的长度，因为出现零树的概率好像比较大，没有论证过，一旦出现零树，它的字节点就不需要再扫描了。而且，教材作者所参考的一篇文献中，也是对上一次结果扫描出的重要数值再次扫描的，仅仅认为是0而已。当然这个不是不妥当的地方，只是与教材作者所参考的文献不一致。
4. 第二次扫描的辅编码错误
在它第二次扫描之后，重新对数值进行了排序，然后对他辅助编码，出来的结果应该是1010 但是，他就直接写了1001，这个是完全错误的。
后记
因为我平时杂事比较多，故此文行文仓促，未能将算法描述详尽，也不免有错误的地方，若有不当之处还请斧正。
在读教材的时候，EZW开篇就出现逻辑错误，我就开始搜集其它地方的资料。由于我们专业对于数学要求不高，先后查阅了Fourier的相关资料，小波变换的相关资料。问了许多同学老师，包括通信学院的张伟鹏，徐寅辰，都给了我很大的帮助。特别是兰州工业高等专科学校的邢教授，在百忙之中回答我的问题，并找了很多有关的资料给我。谢谢你们！
另外，教材上的傅立叶变换部分和小波变换部份都存在问题，无论是连续变换还是离散变换都有点问题。
本文章所用到的文献、图片、包括这篇文章本身都可以在http://heqichen.cn上下载。
2011年5月6日
参考文献
[1].
J. M. Shapiro, “Embedded Image Coding Using
Zerotrees of Wavelet Coefficients,” IEEE Trans. on Signal Processing, Vol. 41,
No. 12, pp. 3445–3462, Dec. 1993.
[2].
Xiaoyan Xu, “Embedded Zero Tree as Image Coding”[OL].
http://www.google.com/url?sa=t&source=web&cd=7&ved=0CEoQFjAG&url=http%3A%2F%2Fciteseerx.ist.psu.edu%2Fviewdoc%2Fdownload%3Fdoi%3D10.1.1.92.1093%26rep%3Drep1%26type%3Dpdf&rct=j&q=Embedded%20Zero%20Tree%20as%20Image%20Coding&ei=fVfCTcvSE4yivgPFht2zAQ&usg=AFQjCNFDv5B0B_DI5nOhzBO6GhxkbVvBSg&sig2=J3pameO8-HyxbRWZBxhj5w&cad=rja
[3].
PolyValens, http://polyvalens.pagesperso-orange.fr/clemens/ezw/ezw.html[OL]
相关下载：
5,301 total views, 6 views today
lilcheery
学长你好，网上翻到这边文章已经过了很多年，不知道你还在用文章里说的那个gmail么？想问一下多媒体技术基础这门课上大的考试一些问题，如果没有用了，可以留下新的邮箱么？